TWiki> Main Web>TWikiUsers>AlexanderFedotov>AVFedotovLogA>AVFedotovLogA002 (revision 3)
Main Web>TWikiUsers>AlexanderFedotov>AVFedotovLogA>AVFedotovLogA002 (revision 3)EditAttachPDF
- Set DISABLEDPLUGINS = LatexModePlugin
- Set LATEXFONTSIZE = footnotesize
Sample Statistics |
1 Population quantities
Let have a probability density function
have a probability density function 
1.1 Moments = Raw Moments = Crude Moments. Mean.
A raw moment (or just a moment, or a crude moment )
is a moment taken about 0 [1] :
(or just a moment, or a crude moment )
is a moment taken about 0 [1] :

 ,
,
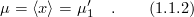
1.2 Central moments and their relations with the raw moment
A central moment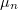 is a moment taken about the mean
is a moment taken about the mean  [2] :
[2] :



 and
and 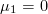 ):
):


1.3 Cumulants and their expressions via moments
The characteristic function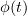 associated with the
probability density function
associated with the
probability density function  is defined as a Fourier transform
[3] :
is defined as a Fourier transform
[3] :
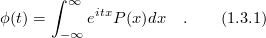
 are then defined by
are then defined by

 :
:
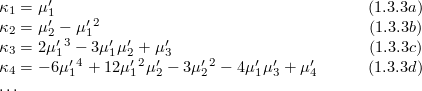
 :
:
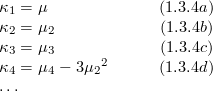
 is the mean and
is the mean and  is the variance.
is the variance.
2 Sample quantities
A sample is a subset of a population [4]
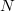 is the size of the sample.
is the size of the sample.
2.1 Power sums
Power sum is the sum of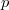 th powers of the sample elements:
th powers of the sample elements:

2.2 Sample raw moments
The th sample raw moment
th sample raw moment  is defined as [5]
is defined as [5]
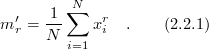


2.3 Sample mean
The sample mean [6] is defined by

 (1.1.2)
(1.1.2)
2.4 Sample central moments
The th sample central moment
th sample central moment 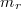 is defined as [7]
is defined as [7]
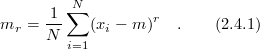
 is the sample mean .
The first few sample central moments are related to power sums
is the sample mean .
The first few sample central moments are related to power sums  by
by

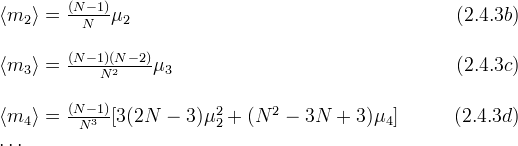
2.5 k-Statistics
The th k-statistic
th k-statistic 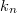 is [8]
the unique symmetric unbiased estimator of the cumulant
is [8]
the unique symmetric unbiased estimator of the cumulant  (see. e.g. eq.(1.3.4)), i.e.,
(see. e.g. eq.(1.3.4)), i.e., 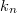 is defined so that
is defined so that

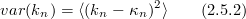
 .
The k-statistics can be given in terms of the power sums (2.1.1)
.
The k-statistics can be given in terms of the power sums (2.1.1)

 (2.3.1)
and central moments
(2.3.1)
and central moments  (2.4.1) by
(2.4.1) by
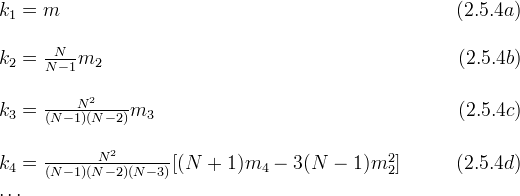

 is given by
is given by

 is given by
is given by

References
[1] Weisstein, Eric W. "Raw Moment." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/RawMoment.htmlTopic revision: r3 - 2010-01-31 - AlexanderFedotov
Webs
- ABATBEA
- ACPP
- ADCgroup
- AEGIS
- AfricaMap
- AgileInfrastructure
- ALICE
- AliceEbyE
- AliceSPD
- AliceSSD
- AliceTOF
- AliFemto
- ALPHA
- Altair
- ArdaGrid
- ASACUSA
- AthenaFCalTBAna
- Atlas
- AtlasLBNL
- AXIALPET
- CAE
- CALICE
- CDS
- CENF
- CERNSearch
- CLIC
- Cloud
- CloudServices
- CMS
- Controls
- CTA
- CvmFS
- DB
- DefaultWeb
- DESgroup
- DPHEP
- DM-LHC
- DSSGroup
- EGEE
- EgeePtf
- ELFms
- EMI
- ETICS
- FIOgroup
- FlukaTeam
- Frontier
- Gaudi
- GeneratorServices
- GuidesInfo
- HardwareLabs
- HCC
- HEPIX
- ILCBDSColl
- ILCTPC
- IMWG
- Inspire
- IPv6
- IT
- ItCommTeam
- ITCoord
- ITdeptTechForum
- ITDRP
- ITGT
- ITSDC
- LAr
- LCG
- LCGAAWorkbook
- Leade
- LHCAccess
- LHCAtHome
- LHCb
- LHCgas
- LHCONE
- LHCOPN
- LinuxSupport
- Main
- Medipix
- Messaging
- MPGD
- NA49
- NA61
- NA62
- NTOF
- Openlab
- PDBService
- Persistency
- PESgroup
- Plugins
- PSAccess
- PSBUpgrade
- R2Eproject
- RCTF
- RD42
- RFCond12
- RFLowLevel
- ROXIE
- Sandbox
- SocialActivities
- SPI
- SRMDev
- SSM
- Student
- SuperComputing
- Support
- SwfCatalogue
- TMVA
- TOTEM
- TWiki
- UNOSAT
- Virtualization
- VOBox
- WITCH
- XTCA
Welcome Guest Login or Register
or Ideas, requests, problems regarding TWiki? use Discourse or Send feedback


